To effectively use photographs for measurement or applications such as Spherical (360°) Panoramas we need to know where the measurements relate to or the point at which the camera and lens system is to be rotated to minimise parallax. For decades this has been referred to as the Nodal Point, but this term is not strictly correct and its use has recently been brought into question. What I find frustrating is that when its use is challenged there is generally no explanation as to why it is not correct or what it should relate to, so I am writing this in defence of the Nodal Point.
 There are probably a variety of reasons why the term Nodal Point is used, but one can be traced back to the use of metric cameras for Close Range or Terrestrial Photogrammetry. In 1921 Heinrich Wild manufactured the Wild P30 Photo Theodolite and during the 19070s and 1980s cameras such as the Wild P31, Wild P32 and Zeiss UMK were used for photogrammetric measurement. These cameras were very large, heavy and expensive with only basic functionality, but had lens systems designed to have virtually no distortion. In the age of the ubiquitous digital computer we can mathematically correct for lens distortion and aberrations, but when restitution was opto-mechanical it was important that no optical errors influenced the result. For example; the Wild P32 had an image size of 90mm x 90mm, cropped to accommodate 120 film, and the lens distortion in the corners was only one or two microns! This was achieved by using “symmetrical” lens systems where the Nodal Point was at the centre and coincided with the Entrance Pupil, Apparent Pupil, Virtual Object, etc. so the term was used correctly. As the computer evolved and became more accessible non-metric cameras could be used for Close Range and Terrestrial Photogrammetry and the point of interest for measurement and the true Nodal Point were no longer necessarily at the same place exactly, but the term stuck.
There are probably a variety of reasons why the term Nodal Point is used, but one can be traced back to the use of metric cameras for Close Range or Terrestrial Photogrammetry. In 1921 Heinrich Wild manufactured the Wild P30 Photo Theodolite and during the 19070s and 1980s cameras such as the Wild P31, Wild P32 and Zeiss UMK were used for photogrammetric measurement. These cameras were very large, heavy and expensive with only basic functionality, but had lens systems designed to have virtually no distortion. In the age of the ubiquitous digital computer we can mathematically correct for lens distortion and aberrations, but when restitution was opto-mechanical it was important that no optical errors influenced the result. For example; the Wild P32 had an image size of 90mm x 90mm, cropped to accommodate 120 film, and the lens distortion in the corners was only one or two microns! This was achieved by using “symmetrical” lens systems where the Nodal Point was at the centre and coincided with the Entrance Pupil, Apparent Pupil, Virtual Object, etc. so the term was used correctly. As the computer evolved and became more accessible non-metric cameras could be used for Close Range and Terrestrial Photogrammetry and the point of interest for measurement and the true Nodal Point were no longer necessarily at the same place exactly, but the term stuck.
A lens has two nodal points, which coincide in a simple lens. These nodal points have the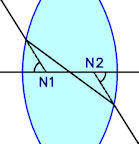 property that a ray of light aimed at one of them will appear to emerge from the other at the same angle relative to the principal ray. A camera lens as not a single lens, but a collection of lenses, or elements as they are called, so does not behave in the same way as a lens. However, the geometry of the rays entering the camera lens and our point of interest is remarkably similar to the behaviour of the front nodal point.
property that a ray of light aimed at one of them will appear to emerge from the other at the same angle relative to the principal ray. A camera lens as not a single lens, but a collection of lenses, or elements as they are called, so does not behave in the same way as a lens. However, the geometry of the rays entering the camera lens and our point of interest is remarkably similar to the behaviour of the front nodal point.
 If we look at a path of light through a lens, such as the fisheye Nikon 10.5mm, we see that although there are the two points, P1 and P2, that the angle the incoming ray subtends with the principal ray is much larger than the angle the exiting ray subtends with the principal ray, which is what we would expect from a fisheye lens. This means that P1 and P2 do not meet the criteria to be defined as Nodal Points as stated in the previous paragraph, but with a camera lens that is actually a set of lenses (elements) there is unlikely to be a condition where this would happen, unless the construction was as used for the metric cameras, so it can be argued that P1 and P2 are the Nodal Points for this particular ray.
If we look at a path of light through a lens, such as the fisheye Nikon 10.5mm, we see that although there are the two points, P1 and P2, that the angle the incoming ray subtends with the principal ray is much larger than the angle the exiting ray subtends with the principal ray, which is what we would expect from a fisheye lens. This means that P1 and P2 do not meet the criteria to be defined as Nodal Points as stated in the previous paragraph, but with a camera lens that is actually a set of lenses (elements) there is unlikely to be a condition where this would happen, unless the construction was as used for the metric cameras, so it can be argued that P1 and P2 are the Nodal Points for this particular ray.
The term node has a wealth of definitions depending on context, but one definition given by my copy of Chambers Twentieth Century Dictionary is “a meeting-point of lines”, which is exactly what we are talking about, and nodal is defined as “of a node or nodes”, so is it really wrong to call our point of interest a Nodal Point? As a node is a point, perhaps the expression nodal point may be tautology, but then language is full of such occurrences.
Although the term Nodal Point, for the point which we are interested in, may not be absolutely correct in optical nomenclature, because it actually has a defined meaning, its recognition of meaning and long term usage should enable its continued use and acceptance. After all, languages are heavily populated with words that have meanings and usage other than their original. Taking one small example; what is your understanding of the word safari? Does it mean a tented camp in the Maasai Mara or being driven through the bush in four wheeled drive vehicle spying on the private lives of African wildlife? Maybe it conjures up images of pith helmeted hunters with heavy bore rifles and teams of porters with large headloads or is it an Internet access provider, particularly if you are an Apple user? The word is actually a Swahili word which simply means “a journey”, which I would be using correctly if I said was going on safari from my home to work, but all the other use are acceptable in today’s world.
One term that appears to be in vogue is to refer to our point of interest as the No Parallax Point (NPP), but this has its own problems. Some lenses, such as the Sigma 10-20mm f4-5.6 EX DC HSM, have a single point where the rays entering the lens apparently converge so this point can indeed be referred to as the No Parallax Point, but what about lenses such as the Sigma 8mm f/3.5 EX DG and Nikon 10.5mm f2.8 G ED fisheye lenses, which have an infinite number of points depending on the angle of the ray entering the lens relative to the principal ray. Where is this No Parallax Point in these cases? If we take the condition that the direction of these rays should coincide where our images “join” when making Spherical Panoramas then this “point” will vary with the number of images used to record the 360° coverage and therefore will no longer be a property of the lens, but also a property of its use.
The following images are an attempt to illustrate the preceding comment and show the angular coverage (FoV) of the Nikon 10.5mm f2.8 G ED and Sigma 10-20mm f4-5.6 EX DC HSM lenses in “portrait” orientation across the width at the centre. The angular coverage (FoV) of course increases as we move up and down from the central axis.
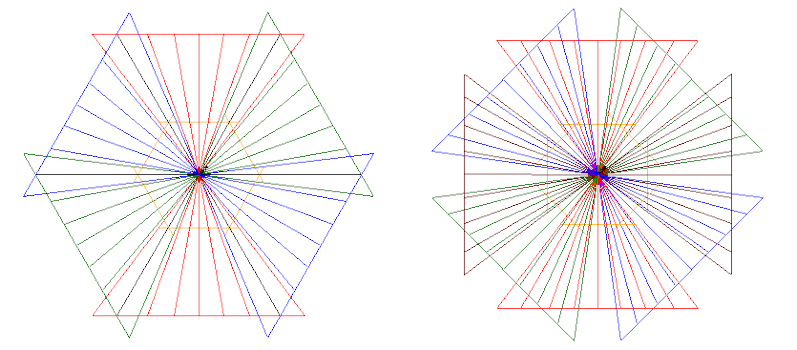
The Sigma 10-20mm f4-5.6 EX DC HSM lens has an Entrance Pupil at a point for a given focal length (e.g. @ 10mm as used in the figures above). This means that the panohead can be set up so that the No Parallax Point (point of rotation) is the same whether 6 images horizontally are recorded at 60° intervals or 8 images at 45° intervals. The diagrams also show the limited overlap with only 6 images @ 60°
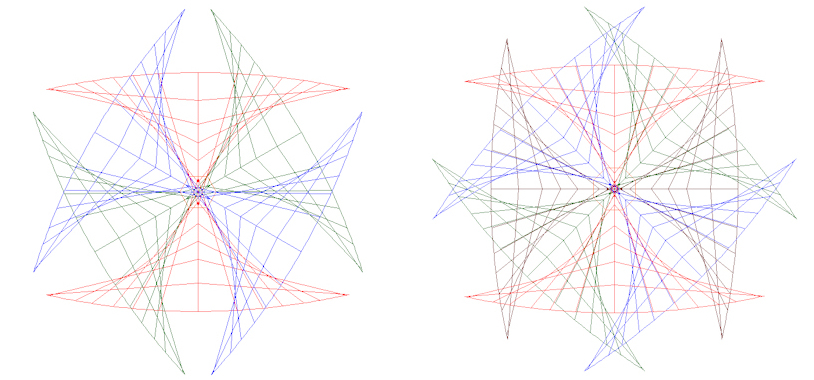
The Nikon 10.5mm f2.8 G ED fisheye lens has an infinite number of points and the point at which the rays entering the lens at 30° from the principal ray (60° separation) is slightly further back from the front of the lens than the point at which the rays entering the lens at 22.5° from the principal ray (45° separation) so the No Parallax Point varies with the number of directions required for the 360° panorama.
Michel Thoby has introduced a more accurate term for our “point of interest”, the Least Parallax Point (LPP). As this refers to a single point where the parallax is a minimum this is the point around which the images are rotated.
The panohead I currently use to make Spherical Panoramas is called a Nodal Ninja so the point around which the camera and lens system rotes in space could be referred to as the Nodal Ninja Point (NNP). This is a true point, so we have a term that is accurate. However, there are a myriad of panoheads available to us so users of other makes, or home made ones, would rightly object to the use of this term, so lets abbreviate it to Nodal Point!
The photograph of the Wild P30 Photo Theodolite is reproduced with the kind permission of the Virtual Museum of the UNSW Surveying Instrument Collection.
