Geoscience Fire Projects
Rationale and Scientific Objectives
The landscape of northern Tanzania is dominated by the East African Rift Valley (EAR) and the Volcanoes of the Crater Highlands: it is a tremendously inspiring place to study Earth Sciences. A largely geophysical project was chosen as traditional BSES geology mapping would have been difficult because outcrops are both scarce dominated by fine-grained lavas and volcaniclastics that are difficult for novice geologists to differentiate in the field. Geology was restricted to making observations about the activity in the active crater of Ol Doinyo Lengai.
The EAR is the topographic expression of plate tectonic forces that are pulling eastern Africa apart. It has one of the strongest gravity anomalies anywhere in the world, and a regional profile was carried out across the rift valley to infill existing data.
Extension causes the continental crust to thin. Hot mantle material wells up underneath the thinned crust, and partially melts as it decompresses. Large-scale faulting of brittle surface rocks occurs, sometimes creating conduits through which magma from the mantle can flow, and volcanism occurs where these conduits are open as far as the earth’s surface. Hence volcanoes are often located along faults, and Northern Tanzania is no exception, with Ol Doinyo Lengai and Keri Maasai both lying along the western bounding fault of the EAR. Lengai is unique for its natrocarbonatite (sodium rich) lavas, the source of which is uncertain, but is thought to involve melting of a contaminant within the shallow crust. A gravity survey of the Lengai was carried out with the aim of constraining its density structure and providing information about the composition of the volcano.
Background
Regional geology
The EAR extends north from Tanzania, through Kenya and Ethiopia to reach the African Coast at Djibouti (Figure 6). It forms one of three limbs of a tectonic plate boundary system which radiates from a triple junction at the southern end of the Red sea. A second arm runs east to the Indian Ocean whilst the third arm continues north along the Red Sea and then up the Dead Sea Transform Fault Zone through Lebanon and Syria to Turkey.
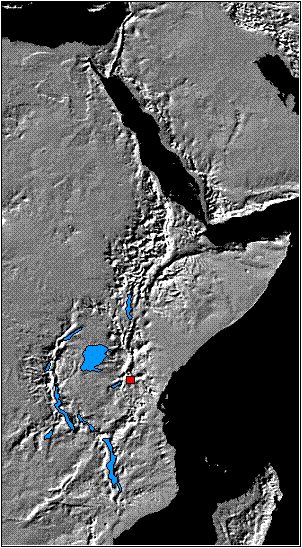 The EAR comprises a chain of individual but linked rift basins which are the expression of subsidence caused by extension of the African continental crust. The ultimate end point of continental rifting is full ocean spreading, and the transition from continental rift to ocean is illustrated by the topographic depression centred on Djibouti: If the plate tectonic forces remain extensional across the EAR then in a few million years the Rift Valley will be a narrow sea like the Red Sea is today.
The EAR comprises a chain of individual but linked rift basins which are the expression of subsidence caused by extension of the African continental crust. The ultimate end point of continental rifting is full ocean spreading, and the transition from continental rift to ocean is illustrated by the topographic depression centred on Djibouti: If the plate tectonic forces remain extensional across the EAR then in a few million years the Rift Valley will be a narrow sea like the Red Sea is today.
Eastern Africa is one of the few places in the world where incipient rifting is expressed on land, and it is accompanied by active volcanism. At its southernmost end the EAR splits into three seismically active arms, marked by lakes where subsidence has resulted from recent extension. One arm runs SW through Lakes Eyasi and Wembere, another SE through Kilimanjaro to the Indian Ocean coast and the third, central arm runs southwards along the Lake Natron – Lake Manyara rift (the study area). Thus does the rifting control the geography: valleys result from extension, lakes flood the valleys, and volcanoes exploit fractures associated with extension and are aligned along the rifts.
The African continental crust is very old, cold and thick and was created in the Precambrian by the suturing together in plate tectonic collisions of continental blocks or cratons (e.g. Ebinger et al. 1997). Collision belts, once the site of mountain chains (the Himalayas are a modern example) remain zones of weakness relative to the cratons. Modern extensional tectonics exploited the weakness of a suture zone east of the Tanzania Craton called the Mozambique mobile belt to create the EAR. Faulting and volcanism began approximately five million years ago in Northern Tanzania. Volcanism commenced in the Early Pliocene along faults bounding the (Lake) Manyara, Natron and Eyasai basins. These faults joined together to form the escarpment at the western edge of the Rift Valley after a major episode of volcanism approximately one million years ago (Foster et al. 1997). Volcanism continues today, with the last major eruption of Lengai having occurred in 1966 and 1967.
Figure 6 Shaded topographic relief map of Eastern Africa and Arabia, showing the African Rift System. The study area is shown in red
Gravity theory and surveys (See Mussett & Khan 2000 or equivalent for more details)
“Big G” and “little g”
Sir Isaac Newton proved that the force of gravitational attraction between two bodies of mass m1 and m2 respectively is:
(equation 1)
where G (“big G”) is the universal gravitational constant (6.672 x 10-11 m3 kg s-3) and d is the distance between their centres of mass. From this the force g of gravitational acceleration at the earth’s surface (“little g”) can be derived as:
(equation 2)
where mearth is the mass of the earth (approximately 5.98 x 1024 kg) and d = distance to the centre of the earth. [For the equatorial radius of 6378km, g works out at the school textbook value of 9.8 ms-2].
Gravity surveys and gravimeters
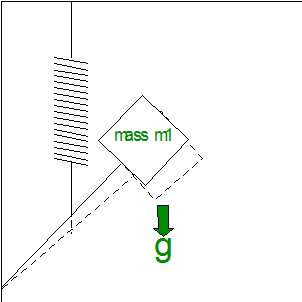 All field gravimeters work on the same principle: they contain a mass on a spring and measure the variation in the length of the spring as the mass responds to variations in g (Figure 7). This simple concept requires precision engineering which results in a $70,000 Instrument.
All field gravimeters work on the same principle: they contain a mass on a spring and measure the variation in the length of the spring as the mass responds to variations in g (Figure 7). This simple concept requires precision engineering which results in a $70,000 Instrument.
A gravity survey is the measurement of the spatial variation in g, from which variations in the near-surface density structure of the earth may be inferred (Figure 8). At the scale of the EAR (approx 100 km across) a survey can be used to infer details only down to 10 km depth or so, a tiny fraction of the 5.98 x 1024 kg mass of the earth. Because it is looking at only a small fraction of the earth, a gravimeter needs to be incredibly accurate, measuring differences much less than a millionth of g.
Figure 7 Schematic of a field gravimeter. The instrument measures the varying length of the spring as it changes in response to changes in g. The instrument is protected from shocks by additional springs and heated to a constant 49°C to prevent temperature-induced variations in response.
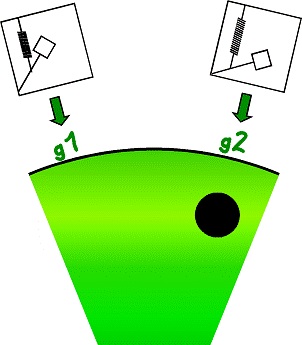 Figure 8 Schematic of a gravity survey. Variations in g caused by local density variations are measured by the gravimeter, In this case g2 > g1 from which the presence of a of a higher density body at location g2 can be inferred.
Figure 8 Schematic of a gravity survey. Variations in g caused by local density variations are measured by the gravimeter, In this case g2 > g1 from which the presence of a of a higher density body at location g2 can be inferred.
Latitude and terrain corrections, or the need for accurate surveying:
Before values of g can be used to make inferences about crustal density variations, four corrections need to be made.
(1) Considering equation 2, the variation in g measured (a) 1m above the equator and (b) at ground level at the equator can be calculated as follows:
(a) (equation 3)
(b) (equation 4)
and is -0.00000307ms-2 (equal to -0.307 mGal or “milligals”) per metre above sea level. Thus there is a variation in g with elevation which must be corrected for. This is known as the free-air correction.
(2) Assuming measurements of g are carried on terrain above sea level, rather than floating in space, there is a correction needed for the additional gravitational attraction of the extra terrain between sea level and the measurement point. This can be approximated by the Bouguer slab correction where is the density of the terrain, usually taken as 2.67 x103 kgm-3 for continental crust, and h is the height in metres above sea level. For every metre of height gained, the Bouguer slab correction is thus:
2 x 3.142 x 6.672×10-11 x 2.67 x 103
= 0.00000119ms-2 or 0.119 mgal
The free-air and Bouguer slab corrections have opposite signs and so to some degree cancel each other out. The overall change in g with height is approximately 0.2 mgal decrease for every meter of topography above sea level. A modern gravimeter is capable of measuring gto an accuracy of approximately 0.01 mgal, which is the variation in gravity caused by a height difference of 5 cm.
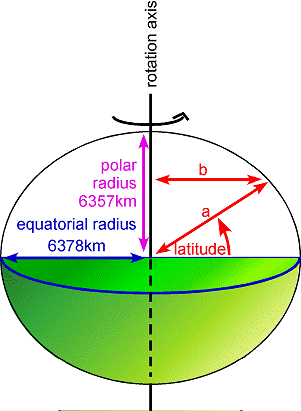
(3) The earth is an oblate spheroid with an equatorial radius of 6378km and a polar radius of only 6357km (Figure 9). This 15km difference causes g measured at the earth’s surface to vary because (a) the earth’s gravitational attraction changes as the distance to the centre of the earth changes, and (b) the centrifugal force felt by bodies at the earth’s surface changes as the distance to the earth’s rotation axis changes. These effects are combined in the International Gravity Formula:
gλ = 978031.8 (1 + 0.0053024 sin2λ – 0.0000059sin22λ) mGal
where gλ is g at latitude λ.
 (4) The Bouguer slab correction above assumes topography above sea level is an infinite smooth plane; the more rugged the terrain is, the less accurate this term becomes. There is a decrease in measured g caused by both the local loss of gravitational pull due to a nearby valley and the negative (upward) pull due to a hill. Both of these can be approximated using the Hammer Terrain Correction (ref). This is done by estimating the variation in elevation relative to the survey point of the neighbouring terrain in a series of expanding concentric circles around the survey point.
(4) The Bouguer slab correction above assumes topography above sea level is an infinite smooth plane; the more rugged the terrain is, the less accurate this term becomes. There is a decrease in measured g caused by both the local loss of gravitational pull due to a nearby valley and the negative (upward) pull due to a hill. Both of these can be approximated using the Hammer Terrain Correction (ref). This is done by estimating the variation in elevation relative to the survey point of the neighbouring terrain in a series of expanding concentric circles around the survey point.
Figure 9 Gravity reading at point P requires correction for latitude. This is because g is proportional to (the square of) the distance to the earth’s centre of gravity a which varies with latitude from 6378 to 6357km, and the centrifugal force due to the earth’s rotation – which acts against g -varies with distance b from the earth’s rotation axis.
Once all of these corrections have been made, the corrected gravity anomaly at a particular point is called the Bouguer anomaly (not to be confused with the Bouguer correction). This is calculated as:
| Bouguer anomaly | = | measured value of g | + | free-air correction |
| – | Bouguer slab correction | – | latitude correction | + | Hammer Terrain correction |
Ewan Laws, Geoscience Fire Leader
